Binary search is an efficient linear search algorithm which is also known as half-interval search or logarithmic search. In this algorithm we try to find the target value inside the linear structure. The range should be sorted in order to apply binary search on it. The middle element is compared recursively until a match is found or the value of least index is not greater then the highest index for the range, which is halved during each recursive call.

Suppose we have to look for a value 76 in a give array say [2, 9, 11, 15, 28, 33, 40, 47, 51, 64, 76, 77, 82, 85, 94]

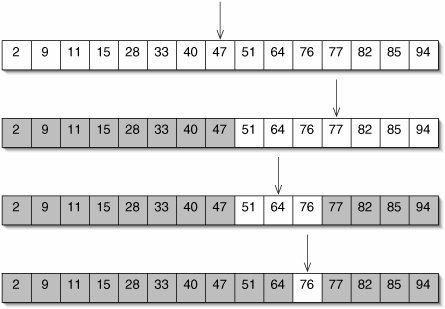
Explanation of the above depicted process

• In the first step mid of the array is calculated having lower index as 0 and higher index at 14, so now mid of 0 and 14 is 7.
• Value at index 7 is 47 which is lower then target value (47 < 76).
• We Need to search in the upper half of the array from index 8 to 14, and now mid of it will be 11.
• Value at index 11 is 77 which is greater then target value (77 > 76).
• We Need to search in the lower half of the array from index 8 to 10, and now mid of it will be 9.
• Value at index 9 is 64 which is greater then target value (64 < 76).
• We Need to search in the upper half of the array from index 10 to 10, and now mid of it will be 10.
• Value at index 10 is 76 which is equal to the target value (76 = 76).

Algorithm for Binary search

• Sort the range in increasing order
• find if lower index is less then higher index, if not then value does't exist in the given range. 
• find mid of the range
• if value at mid is equal to target value then return the answer
• if value at mid is greater than target value, then we have to search in lower half of the range.
• if value at mid is lesser then target value, then  we have to search in the upper half of the range.
   

Sample Demo program of Binary Search algorithm
 

package com.tech.blog;

import java.util.Arrays;
import java.util.Scanner;

public class BinarySearch {
	public static void binSearch(int[] arr, int low, int high, int val) {
		if (low <= high) {
			int mid = (low + high) / 2;
			if (arr[mid] == val) {
				System.out.println("Found at index " + mid);
			} else if (val > arr[mid]) {
				binSearch(arr, mid + 1, high, val); // as target value would present 
                                                    // in between the range   
			} else if (val < arr[mid]) {
				binSearch(arr, low, mid - 1, val); // as target value would present 
                                                   // in between the range
			}
		} else {
			System.out.println("Not found");
		}
		return;
	}

	public static void main(String[] args) {

		int size, num;
		Scanner sc = new Scanner(System.in);

		System.out.print("Insert size of your array : ");
		size = sc.nextInt();
		int[] arr = new int[size];
		System.out.print("Insert your array : ");
		for (int i = 0; i < size; i++)
			arr[i] = sc.nextInt();

		System.out.print("Your sorted array : ");
		Arrays.sort(arr); // here sorting is applied as needed for binary search
		for (int a : arr)
			System.out.print(a + " ");
		System.out.println();
		System.out.print("Enter the value to be searched inside the array : ");
		num = sc.nextInt();

		binSearch(arr, 0, size - 1, num); // call to binSearch method
		sc.close();
		
		return;
	}
}

Output for the given program

Insert size of your array : 15
Insert your array : 2 9 11 15 28 33 40 47 51 64 76 77 82 85 94
Your sorted array : 2 9 11 15 28 33 40 47 51 64 76 77 82 85 94
Enter the value to be searched inside the array : 76
Found at index 10

Insert size of your array : 15
Insert your array : 2 9 11 15 28 33 40 47 51 64 76 77 82 85 94
Your sorted array : 2 9 11 15 28 33 40 47 51 64 76 77 82 85 94 
Enter the value to be searched inside the array : 12
Not found

Time Complexity for binary search is O(log n) where n is the number of elements in the range.

The idea is simple, implementing this algorithm correctly requires attention to some subtleties about the exit condition and the midpoint calculation.

Thanks,

Source: https://en.wikipedia.org/wiki/Binary_search_algorithm